References and useful ressources

• https://arxiv.org/abs/1706.03762
• https://www.youtube.com/watch?v=zxQyTK8quyY
• https://www.youtube.com/watch?v=bQ5BoolX9Ag
• https://levelup.gitconnected.com/understanding-transformers-from-start-to-end-a-step-by-step-math-example-16d4e64e6eb1

What is a Transformer?

Transformers are a type of machine learning model designed for processing sequences. They were introduced in the paper "Attention Is All You Need". The original paper focus on NLP tasks, but it can be applied to other types of data as well.

Motivations

• Limit the lengths of signal paths required to learn long-range dependencies
• Recurrent models do not allow parallelisation within training examples

Model architecture

Unlike RNN models, Transformers doesn't process inputs sequentially.

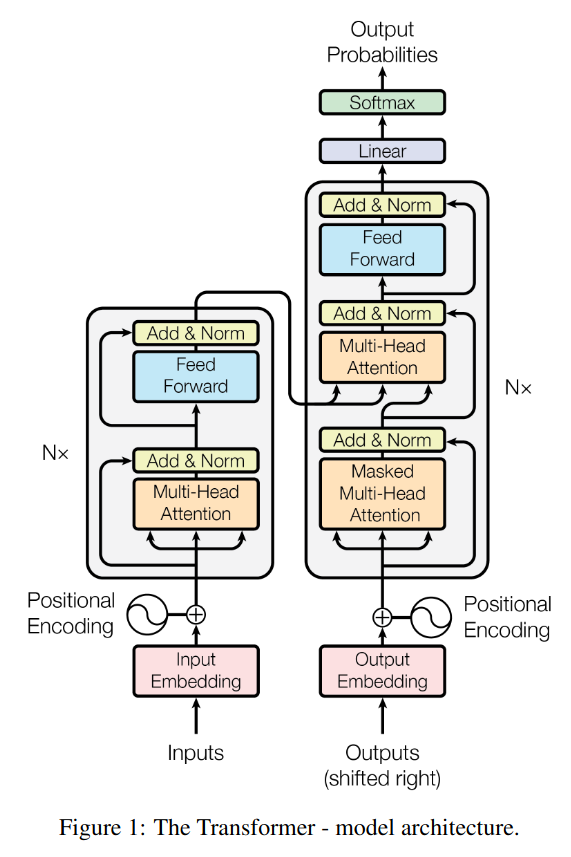
The Transformer follows this overall architecture using stacked self-attention and point-wise, fully
connected layers for both the encoder and decoder, shown in the left and right halves of Figure 1,
respectively.

Encoder: The encoder is composed of a stack of N = 6 identical layers.

• Each layer has two sub-layers. The first is a multi-head self-attention mechanism, and the second is a simple, position-wise fully connected feed-forward network.
• We employ a residual connection around each of the two sub-layers, followed by layer normalization (To facilitate these residual connections, all sub-layers in the model, as well as the embedding layers, produce outputs of dimension dmodel = 512)

Decoder: The decoder is also composed of a stack of N = 6 identical layers.

• Each layer has three sub-layers. The first is a multi-head self-attention mechanism, the second is a simple, position-wise fully connected feed-forward network and the third is a layer, which performs multi-head attention over the output of the encoder stack.
• We employ a residual connection around each of the two sub-layers, followed by layer normalization.
• We also modify the self-attention sub-layer in the decoder stack to prevent positions from attending to subsequent positions. This masking, combined with fact that the output embeddings are offset by one position, ensures that the predictions for position i can depend only on the known outputs at positions less than $i$.

Ancestors of the Transformers:

• Recurrent neural networks (RNN),
• Long short-term memory,
• Gated recurrent neural networks,
• Convolution neural networks.

⚠️ TODO: complete and explain

Word Embedding

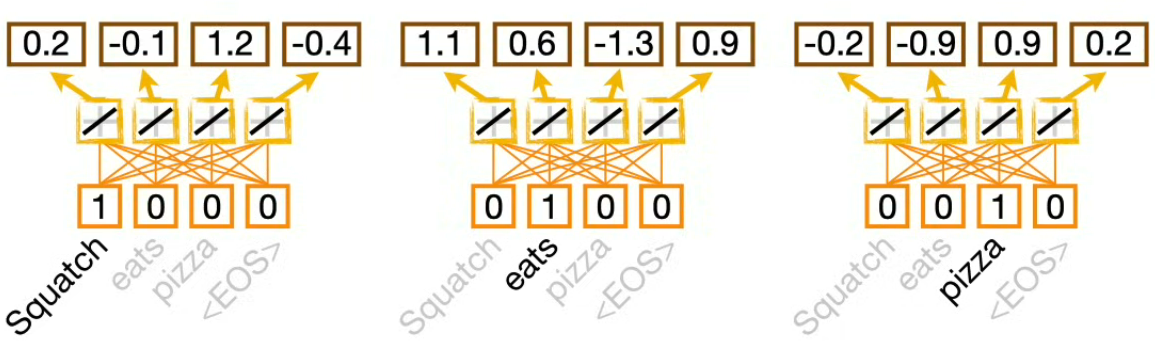
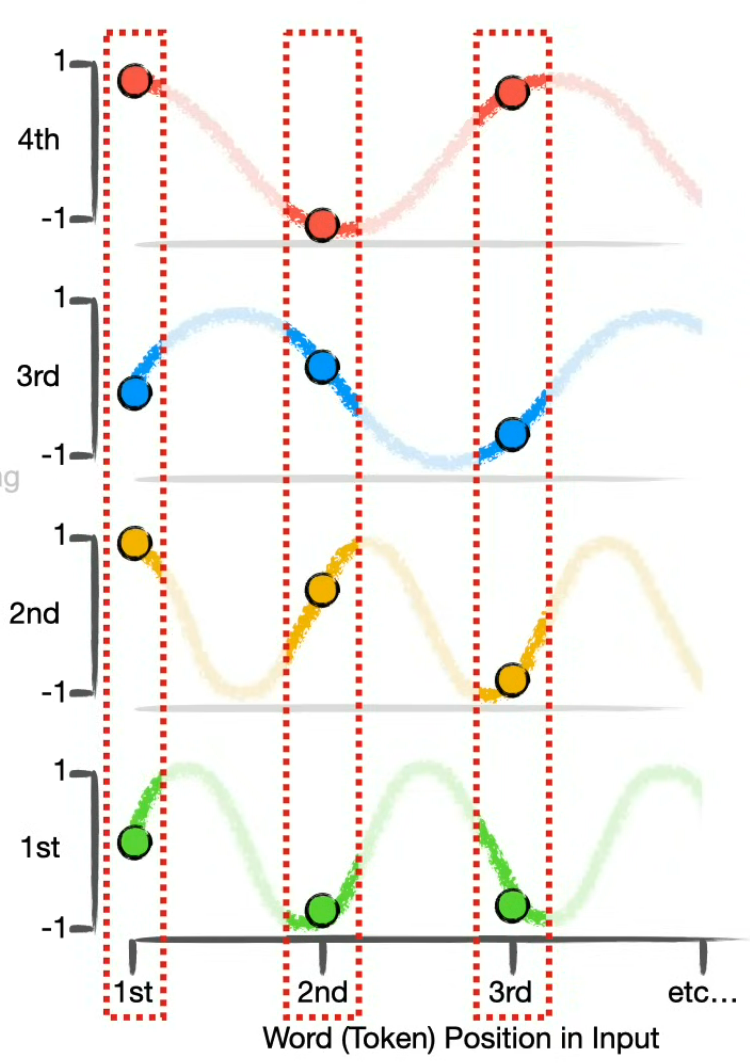
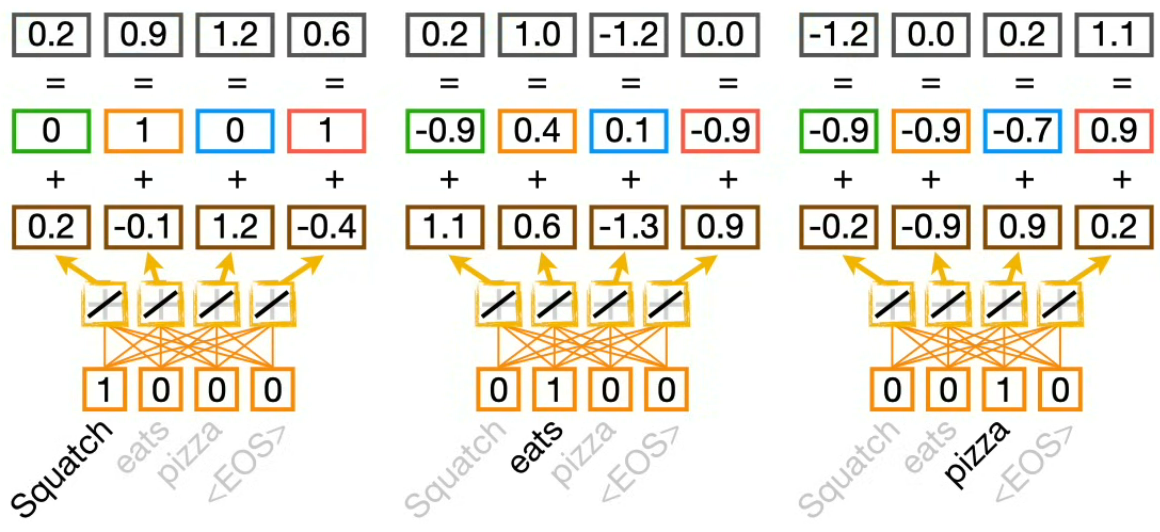
Positional encoding

To compute the positional encoding, we use the cos and sin graphs with various wavelengths. The number if positional encoding graphs match the embedding dimensionality. And finally the positional embedding is added to the word embedding.

⚠️ We use the same cos and sim graphs for the encoding and decoding parts of the Transformer.

Self attention

It works by seeing how similar each word is to all of the words in the sentence (including itself).

It's done with all the tokens indeed

Compute similarity scores

(for all tokens)

Words that are more often associated and proximate to each others in text corpus will get higher similarities (e.g. "it" and "pizza" or "it" and "oven" will have high scores, whereas "The" and "came" will not). And these similarity scores are used to compute the Query and Key values.

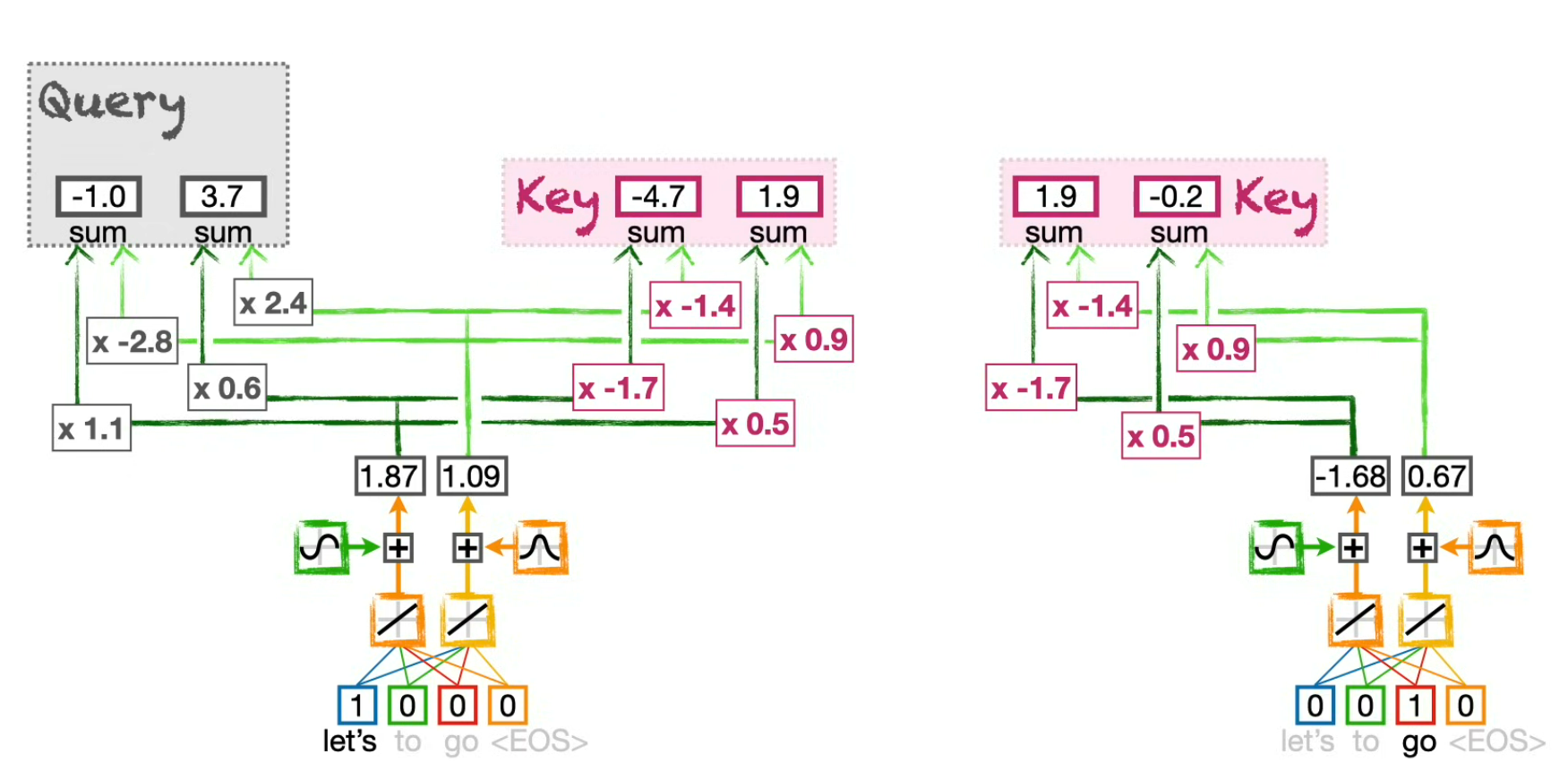
Compute Query and Keys

(for the token "Let's")

1. we compute the Query value for "Let's"
2. we compute the Key value for "Let's"
3. we compute the Key value(s) for the other tokens of the sentence.

⚠️ We use only one set of weight to compute all Keys and only one set of weight to compute all Queries (in fact, one for the Encoder Self-Attention, one for the Decoder Self-Attention and one for the Encoder-Decoder Attention), but as we apply them on different positional encodings, the results are different.

At the bottom we can see the input, then the embedding, then the position encoding (with the cos and sin symbols), then the result of the word and position encoded values... finally of top of all of these, we can spot the similarity scores used to compute the Query and Key values.

Compute the Dot Product similarity between the Query and the Keys

(for the token "Let's")

This is simply done by applying any similarity function between the Query and each Key.

The orignal paper use: $Sim=\frac{\text{Dot product}}{\sqrt{\text{embedding size}}}$ but in this example we use Dot product for simplicity.
e.g. $(-1.0\times -4.7)+(3.7\times 1.9)=11.7$ and $(-1.0\times 1.9)+(3.7\times -0.2)=-2.6$

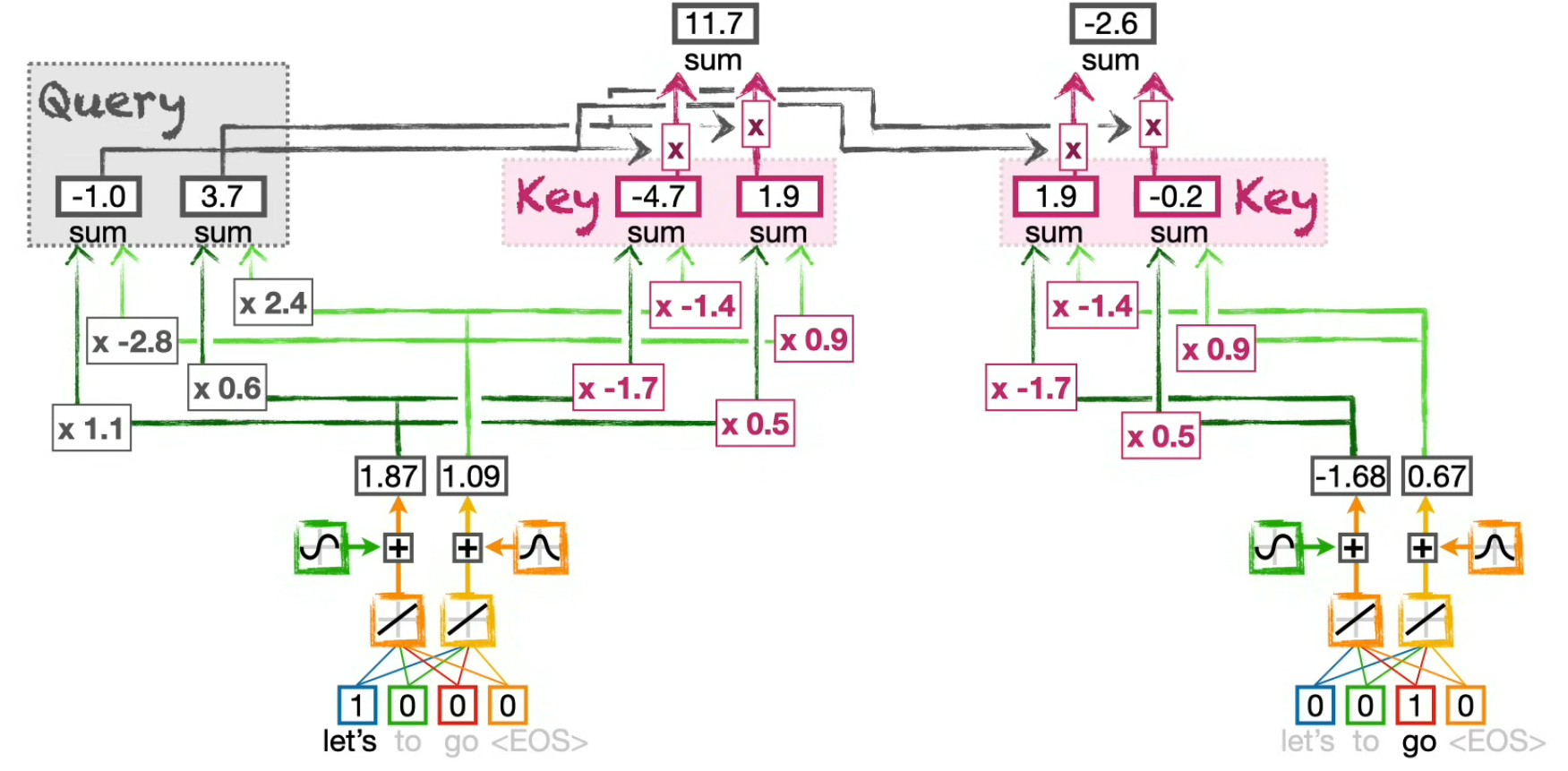
We can see that "Let's" is more similar to itself (11.7) than to "go" (-2.6)

Compute the influence of each tokens on the current token

(in this case the "current" token is "Let's")

We use a softmax function (which sums up to 1.0) to compute how much each token should influence the final Self-attention score for this particular token.
e.g. $softmax(11.7,-2.6)=[1.0,0.0]$

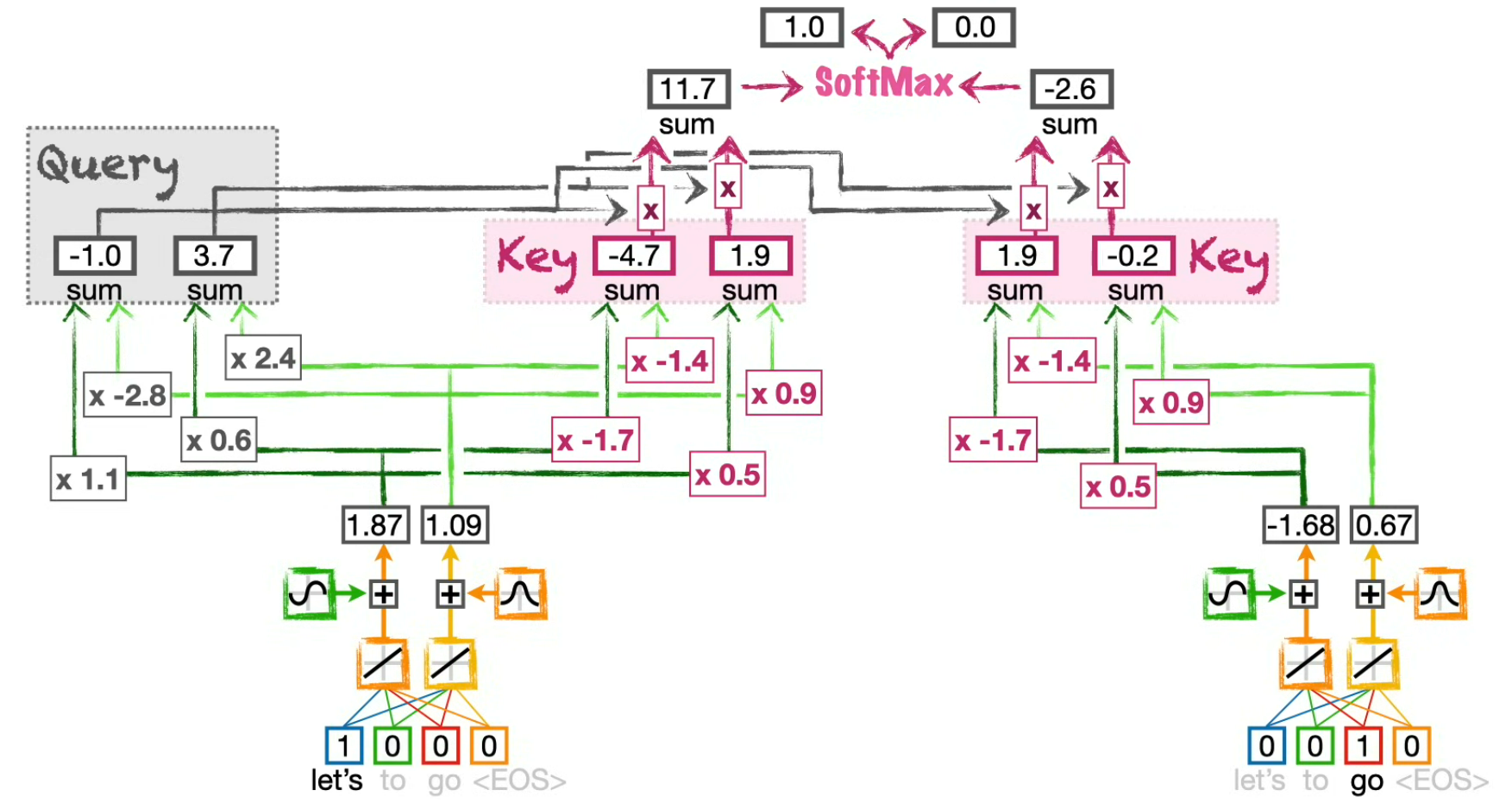
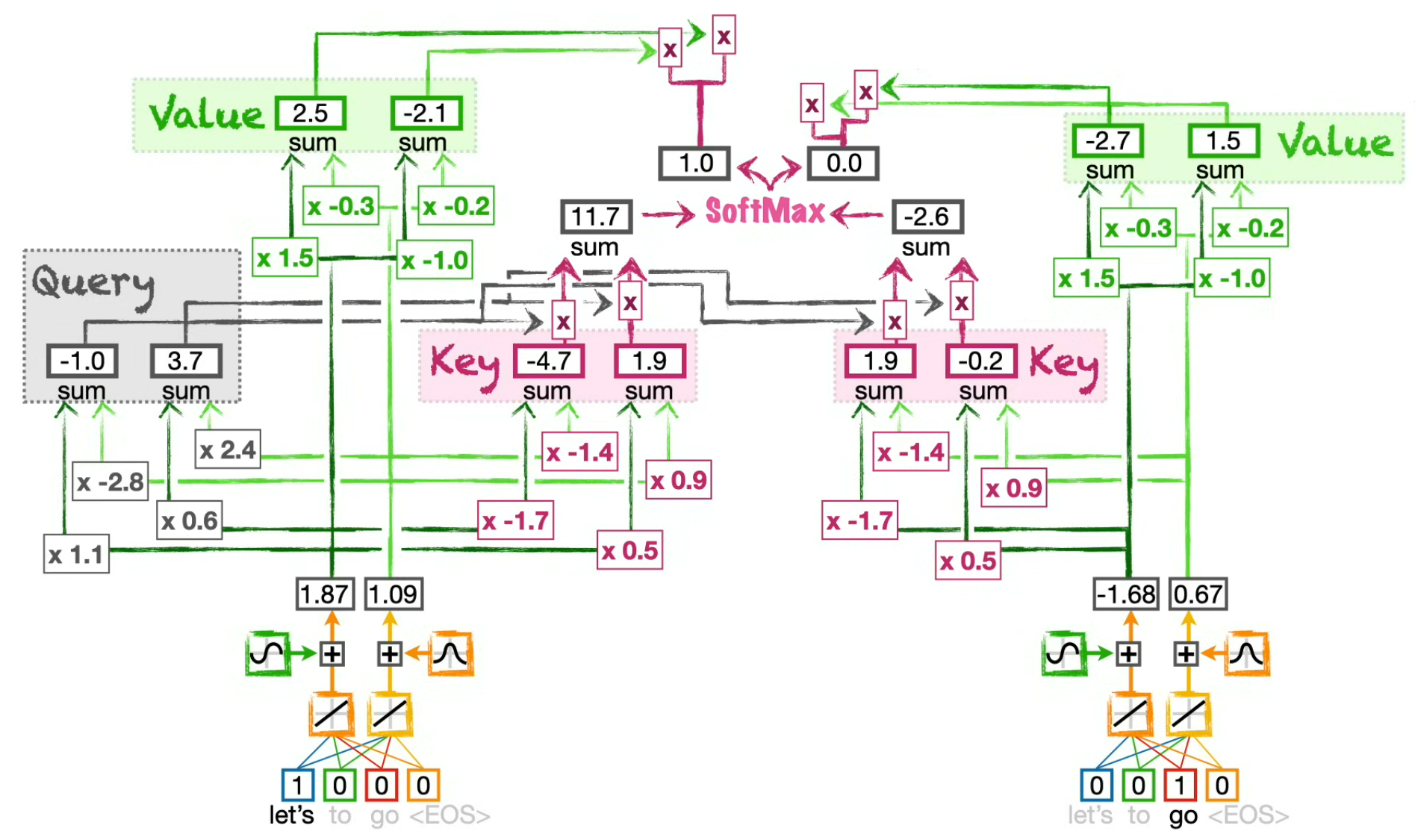
Compute the token Value to be influenced

(for the token "Let's" on this schema, but in fact we do it for all tokens at the same time)

Now that we know how much each token of the sentence can influence the current token value, we need to actually get a Value to influence...

⚠️ We use only one set of weight to compute all Values (in fact, one for the Encoder Self-Attention, one for the Decoder Self-Attention and one for the Encoder-Decoder Attention), but as we apply them on different positional encodings, the results are different for each token.

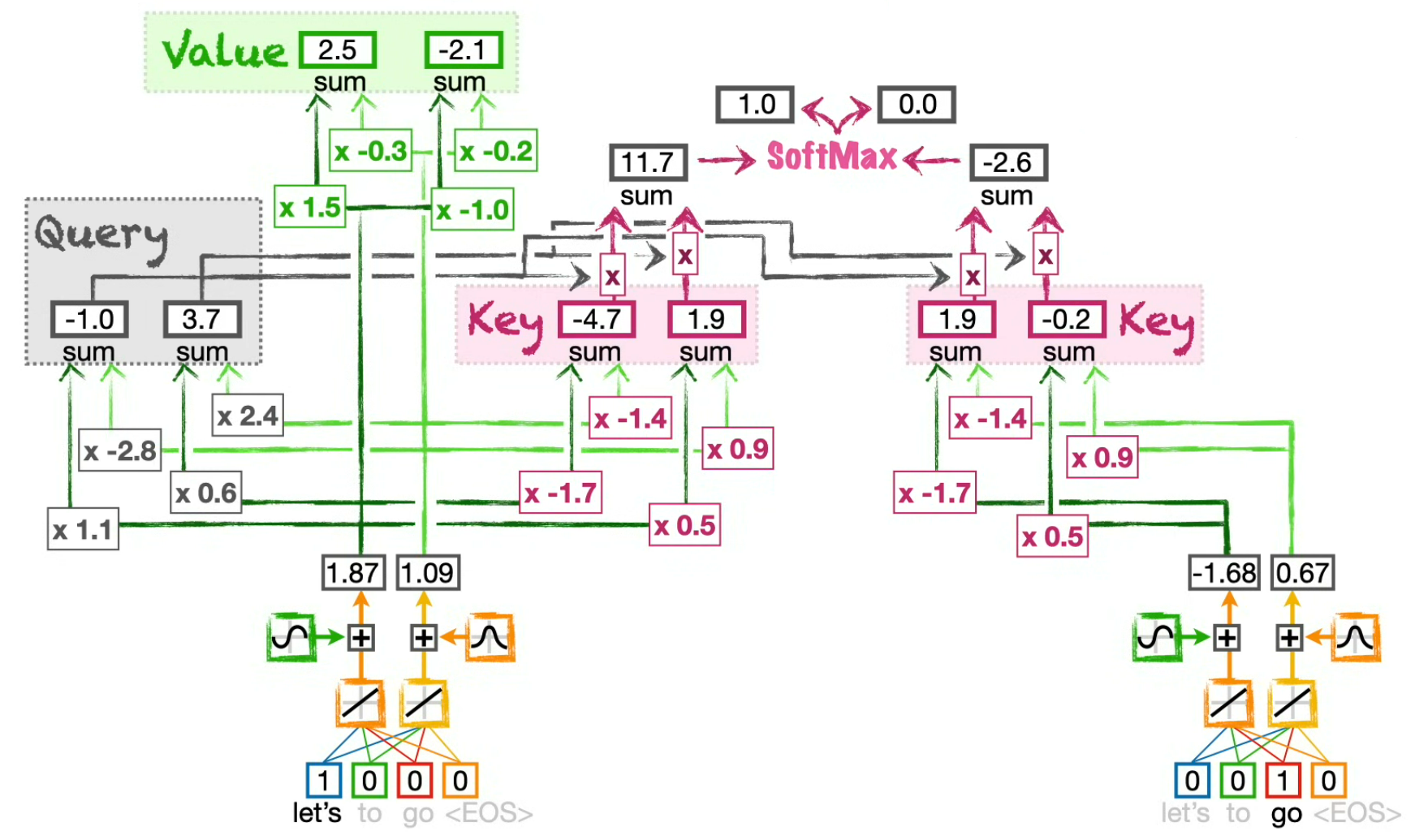
Compute the influenced intermediary embeddings by scaling the values

(for all tokens)

Here, we use the influence ratio on the current token Value to get intermediary values...
e.g. $[(2.5\ast 1.0),(-2.1\ast 1.0)]=[2.5,-2.1]\text{ and }[(-2.7\ast 0.0),(1.5\ast 0.0)]=[0.0,0.0]$

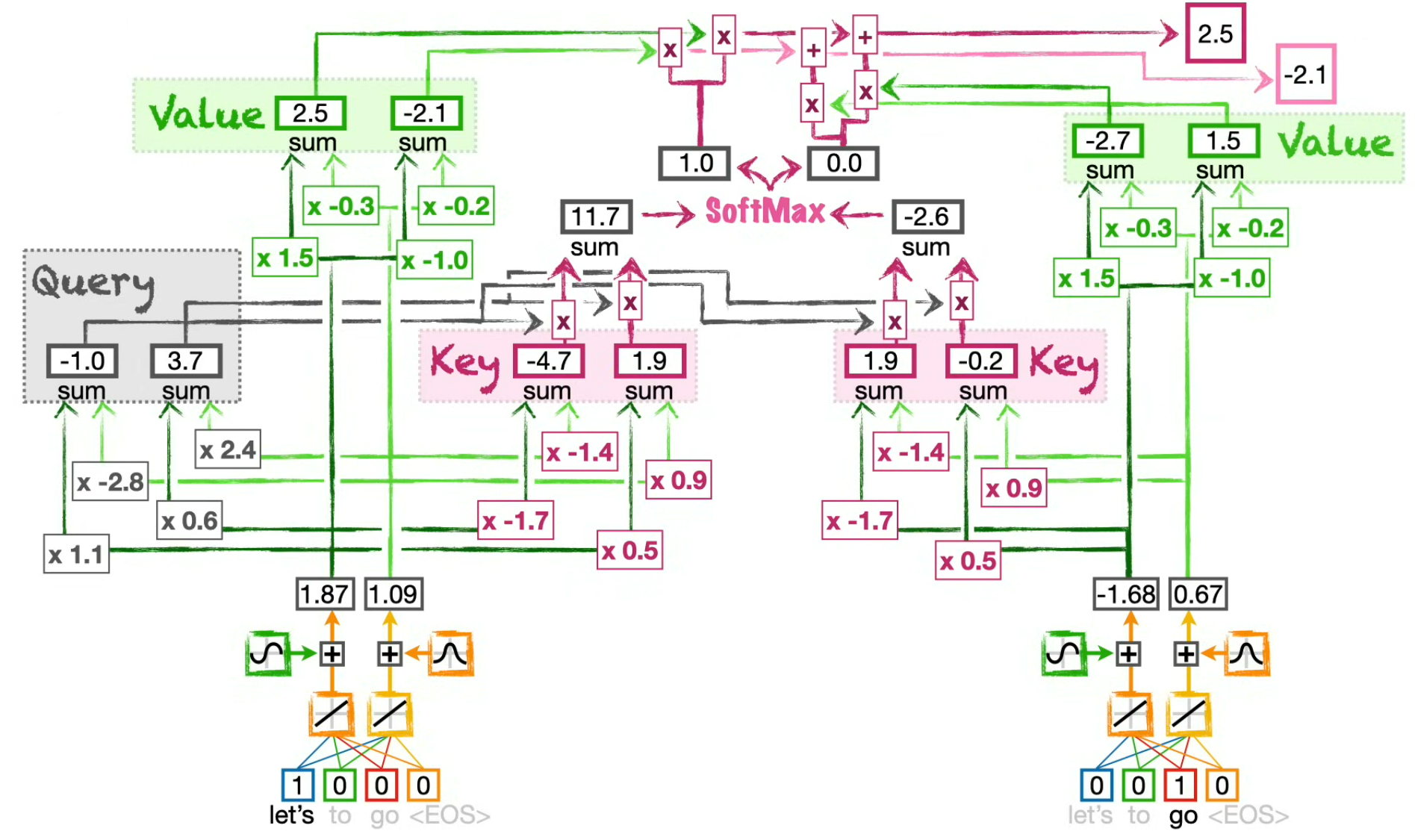
Compute the Self-attention values

(for the token "Let's")

Finally, by summing the intermediary embeddings for all tokens of the sentence, we compute the Self-attention values for the current token.
e.g. $[2.5,-2.1]+[0.0,0.0]=[2.5,-2.1]$

Repeat for the next tokens in the sentence...

Now that we have computed the Self-attention values for the current token, it's time to start over with the next token and the next one etc. until the end of the sentence.

⚠️ But, no matter how many words are input in the Transformer we can just reuse the same sets of weights for Queries, Keys and Values inside a given Self-Attention unit (in fact need one of each for the Encoder Self-Attention, one of each for the Decoder Self-Attention, and one of each for the Encoder-Decoder Attention).

So once we computed the values for the first token, we don't need to recalculate the Keys and Values for the others, only the Queries. And then we do the math to get the Self-attention values.

1. Compute the Dot Product similarity between the Query and the Keys
2. Compute the influence of each tokens on the current token (using SoftMax)
3. Compute the influenced intermediary embeddings by scaling the values
4. Compute the Self-attention values

However, we don't really need to compute them sequentially. Transformers can take advantage of parallel computing, so we can compute the Queries, Keys and Values all at the same time using vectorization.